[논문] Attention Is All You Need - Transformer 모델

 

Attention Is All You Need

내 인생 첫 논문! Transformer 모델의 시작인 논문으로 너에게 필요한 모든 것은 Attention만이다. 제목으로 시작한다.

1. Introduction

기존의 RNN, LSTM, GRU 기반의 모델들은 순환 모델이고, 순환모델은 병렬처리가 불가능하다는 점과 시퀀스 크기가 제한되어 있는 단점들이 존재했다.
Attention은 기존에도 존재했지만 RNN 모델과 함께 사용하는 형태로만 쓰였기때문에 단점은 여전히 존재했다.

Transformer는 기존 순환모델들을 전혀 사용하지 않고, 오로지 Attention 만을 이용해서 만들어진 모델로 비순환 모델이다.
비순환 모델은 순환모델들이 가지고 있던 단점들을 개선하고 병렬처리가 가능하여 속도도 훨씬 빨라졌다.

2. Background

기존 순환모델들은 index 0부터 last index까지 순서대로 진행되는데,
그 과정에서 n번째 단어를 학습할 때 n-1번째 hidden state(은닉 상태)가 필요하다. 그렇기때문에 병렬로 불가능하고 직렬로만 가능한 것.

Transformer는 전체 단어들의 가중치를 계산하여, 해당 문장에서 얼마나 중요한 단어인지, 빠져도 되는 단어인지 알 수 있도록 한다.
속도는 빨라졌지만,,, 모두 중요한 단어들이거나 순차적인 의도가 담긴 문장이거나 할 때, 가중치가 낮다는 이유만으로 비중이 줄어드는 경우가 발생했다.

-> Transformer는 이런 단점을 Multi-Head Attention으로 해결했다.

3. Model Architecture

출처 : Attention Is All You Need

Inputs : ["Hello", ",", "how", "are", "you", "?"]

Outputs(shifted right) : 첫번째 토큰 <SOS> (Start Of Sentence)으로 시작해서 <EOS> (End Of Sentence) 토큰이 예측될 때까지 반복한다.
["<SOS> "] -> ["<SOS>", "Hallo"] -> ["<SOS>", "Hallo", ","] ->  ["<SOS>", "Hallo", ",", "wie"]  -> ... -> ["<SOS>", "Hallo",...,"<EOS>"]

3.1 Encoder and Decoder Stacks

Encoder는 두 개의 sub-layer를 가진다.
1. multi-head self-attention
2. positionwise 완전 연결 feed-forward 네트워크
각 두 개의 sub-layer 주위에 residual connection을 사용하고 그 뒤에 layer normalization을 적용한다.

Decoder는 인코더 계층의 두 개 sub-layer + 세번째 sub-layer를 가진다.
3. 인코더 스택의 출력에대해 multi-head attention을 수행한다.
또한, 디코더 스택에서 Output Embeddings이 한 위치만큼 오프셋된다는 사실과 결합되어 위치 i에대한 예측이 i보다 작은 위치에서의 알려진 출력에만 의존할 수 있도록 보장한다.

3.2 Attention

Attention 함수는 query와 key-value 쌍의 집합을 출력에 매핑한다. query, keys, values, output 모두 벡터이다.

출처 : Attention Is All You Need

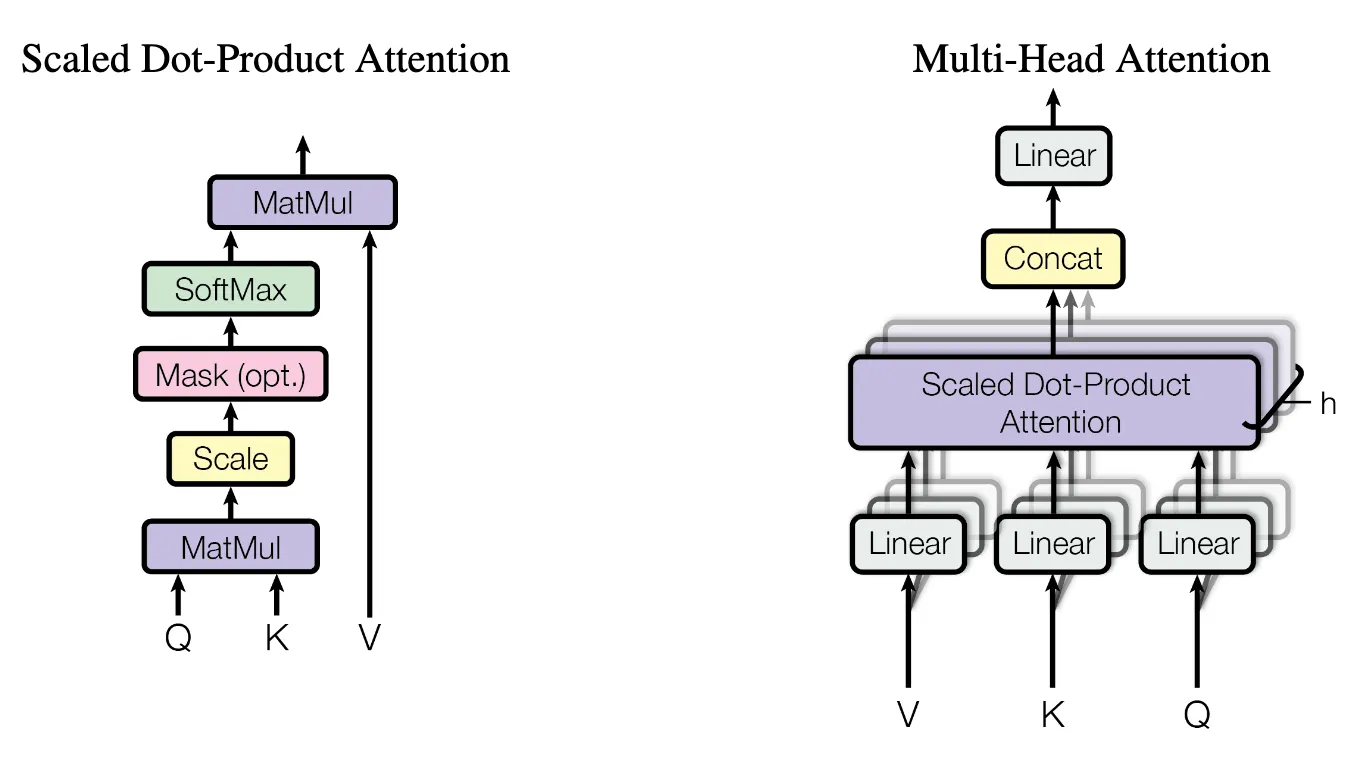
3.2.1 Scaled Dot-Product Attention

$$\text{Attention}(Q, K, V ) = \text{softmax}( \frac{QK^T} {\sqrt{d_k}})V$$

Q와 K의 두 벡터의 내적값을 구해 특정 query가 어떤 key에 얼마나 관심을 가져야하는지 측정할 수 있다.
$\frac{QK^T}{\sqrt{d_k}}$ 내적값이 너무 커지면 softmax 함수는 입력 값을 매우 크거나 작은 값으로 만들게 되므로
$\sqrt{d_k}$ 로 나눠준다.

$\sqrt{d_k}$로 나눠주는 이유는❓

내적값을 $\sqrt{d_k}$ 로 나눠야 분산이 1로 정규화가 되고, 분산이 1이라는 것은 표준편차도 1이기때문에 softmax 과정의 안정성을 보장할 수 있다.

softmax 활성화 함수 사용과 V 곱하기

softmax 활성화 함수는 내적값들을 0.0~1.0 사이 값으로 변환시키고 그 모든 값의 합은 1.0이다.
-> softmax로 인해 변환된 값들은 확률값을 의미.
-> 변환된 값들에 V를 곱하면, value가 해당 문장에서 얼마나 중요도 확률을 가지고 있었는지 알 수 있음.

3.2.2 Multi-Head Attention

Linear Projection (선형 투영)

선형 투영은 한 공간에 있는 벡터를 다른 공간으로 변환하는 수학적인 연산.
→ 차원을 바꾼다.
→ 원본 데이터의 정보를 유지하면서, 다른 특성을 강조하거나 새로운 관점에서 데이터를 볼 수 있게 변환한다.

쿼리(Query)의 선형 투영: $ Q W^Q_i $
키(Key)의 선형 투영: $ K W^K_i $ 값(Value)의 선형 투영: $ V W^V_i $

$$ \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O $$

Concat : 현재 분리되어 있는 여러 Attention Head들의 출력을 하나로 모으는(concatenating) 역할

3.2.3 Applications of Attention in our Model

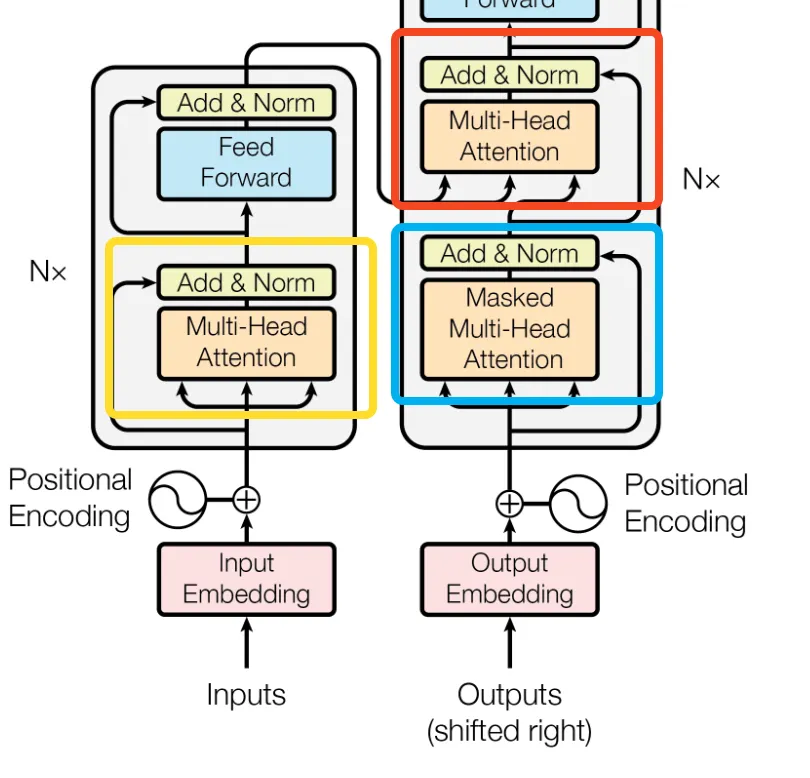
Encoder-Decoder Attention Layer

Encoder에서 Decoder로 z를 넘긴다.
z는 하나의 시퀀스 형태의 연속적인 표현(sequence of continuous representations)을 가지며, 입력 시퀀스의 각 단어에 대한 문맥 정보와 위치 정보가 모두 인코딩된 고차원 벡터들의 시퀀스이다.

Decoder의 Encoder-Decoder Attention Layer에서, 인코더의 최종 출력 z 전체가 Key(K)와 Value(V)로 사용된다.

Query는 이전 Decoder 레이어에서 가져온 값으로 처리.

Encoder의 Self-Attention Layer

Decoder의 Self-Attention Layer

auto-regressive 속성에 의해 디코더에서 왼쪽방향(학습되지 않은 미래 토큰들)로 정보 흐름을 방지한다. 미래 토큰들을 아주 작은 $-\infty$값을 설정해 softmax 결과값을 0에 수렴하는 값이 나오게 한다.

3.3 Position-wise Feed-Forward Networks (FFN)

This consists of two linear transformations with a ReLU activation in between.
두 개의 linear transformation으로 구성되어있는데 사이에 ReLU 활성화 함수가 있다.

FFN Transformer의 Encoder와 Decoder 레이어에 모두 사용되며, Multi-Head Attention의 출력에 비선형성을 추가하고 모델의 표현력을 높이는 역할을 한다.

3.4 Embeddings and Softmax

토큰을 벡터로 변환 : 연속적인 벡터 표현으로 변환한다. 입력 토큰과 출력 토큰 모두 dmodel 차원의 벡터로 변환한다.

In the embedding layers, we multiply those weights by $\sqrt{d_{model}}$ .
임베딩 계층에서 해당 가중치에 $\sqrt{d_{model}}$ 를 곱한다.

3.5 Positional Encoding

we must inject some information about the relative or absolute position of the tokens in the sequence.
모델이 sequence의 순서를 활용하기 위해서는 sequence에서 토큰의 상대적 또는 절대적 위치에 대한 정보를 주입해야 합니다.

Positional encodings는 Embedding과 동일한 차원인 dmodel을 가지므로, 두 값을 합산할 수 있다.

Positional encodings는 짝수일 때 sin, 홀수일 때 cos 계산법을 통해 두 토큰의 상대적 거리를 알 수 있다. 정확한 위치값은 없으나 각 토큰들의 상대적 거리를 통해 토큰 순서를 유추해낼 수 있다.